Ознакомьтесь с конспектом лекций и учебником. Запустите программу компьютерного моделирования. Выберите модель «Взаимодействие точечных зарядов». Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект.

• Знакомство с электрическим полем, создаваемым точечными источниками, и его моделированием.
• Экспериментальное подтверждение закономерностей для электрического поля точечного заряда и электрического диполя (ЭД).
• Экспериментальное определение величины электрической постоянной.

Электромагнитным полем (ЭМП) называется особая форма материи, посредством которой осуществляется взаимодействие между электрически заряженными телами (электромагнитное взаимодействие).

Электрическим полем (ЭП) называется частная форма ЭМП, проявляющаяся в том, что в области пространства, окружающей электрически заряженный объект, на другой заряженный объект действует сила, не зависящая от скорости движения объектов и называемая электрической (кулоновской).

Источником ЭП являются электрически заряженные объекты.

Зарядом (электрическим) называется особая характеристика объекта, определяющая его способность создавать ЭП и взаимодействовать с ЭП. Часто для сокращения текста «зарядом» называют заряженную частицу, а «точечным зарядом» – материальную точку, имеющую электрический заряд.

Основные свойства электрического заряда (как характеристики объекта):

• Заряд инвариантен – его величина одинакова при измерении в любой инерциальной системе отсчета (иногда для краткости говорят «заряд не зависит от скорости»).
• Заряд сохраняется – суммарный заряд изолированной системы тел не изменяется.
• Заряд аддитивен – заряд системы тел равен сумме зарядов отдельных тел.
• Заряд дискретен – заряд любого тела по величине кратен минимальному заряду, который обозначается символом е и равен 1,6∙10^–19 Кл.
• Существуют заряды двух разных «сортов». Заряды одного «сорта» названы положительными, а другого «сорта» – отрицательными. Одноименные (одного «сорта») заряды отталкиваются, а разноименные – притягиваются.

Если вблизи одной заряженной частицы (далее обозначаемой как Q₁), расположенной в начале координат в вакууме, будет находиться вторая заряженная частица (заряд Q₂), то на второй заряд будет действовать электрическая (кулоновская) сила 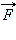, определяемая законом Кулона:

где 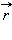– радиус-вектор точки наблюдения, 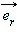– единичный радиус-вектор, направленный в точку расположения второго заряда, 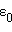– электрическая постоянная, ε – диэлектрическая проницаемость среды.

Напряженность электрического поля – характеристика силового воздействия ЭП на заряд. Напряженность ЭП, создаваемого зарядом Q₁, есть векторная величина, обозначаемая символом (Q₁) и определяемая соотношением

где 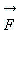– сила, действующая на заряд .

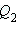Величина напряженности ЭП точечного заряда, расположенного в начале координат, равна

После логарифмирования этого выражения получим

Линия ЭП (силовая, напряженности) – линия, в любой точке которой вектор напряженности ЭП направлен по касательной к ней.

ЭП подчиняется принципу суперпозиции: напряженность ЭП нескольких источников (зарядов) является суммой векторов напряженности поля, создаваемого независимо каждым источником: .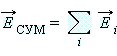

Потоком ЭП называется интеграл по некоторой поверхности S от скалярного произведения напряженности ЭП на элемент поверхности:

где вектор направлен по нормали к поверхности.

Закон (теорема) Гаусса для ЭП: поток ЭП через замкнутую поверхность S₀ пропорционален суммарному заряду, расположенному внутри объема V (S₀), ограниченного поверхностью S₀ интегрирования потока:

Линии напряженности электрического поля, созданного уединенным точечным зарядом, представляют собой прямые линии. Они идут от заряда, если он положительный, и к заряду, если он отрицательный.

Потенциалом данной точки 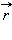ЭП называется скалярная характеристика ЭП, численно равная работе сил поля по перемещению единичного положительного заряда из данной точки в другую фиксированную точку 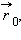в которой потенциал принят за 0 (например, если возможно, то в бесконечность):

Уравнение, выражающее напряженность через потенциал:

где оператор градиента

Диполь – два одинаковых по величине, но противоположных по знаку, точечных заряда Q, расположенных на расстоянии L (L – плечо диполя).

Дипольный (электрический) момент – есть произведение

Вектор дипольного момента 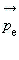направлен от отрицательного к положительному заряду.

Напряженность ЭП диполя вычисляется с использованием принципа суперпозиции для ЭП.

Как видно из рис. 1, 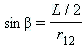, а для модуля суммарной силы получим

На линии, проходящей через центр диполя, перпендикулярно электрическому моменту, и на большом расстоянии r от его центра:

Величина напряженности электрического поля диполя на указанной линии

После логарифмирования этого выражения получим

Модель взаимодействия двух точечных зарядов

Подготовьте табл. 2 и 3, используя образцы.

Таблица 1 (не перерисовывать). Значения величины заряда Q₁

Таблица 2. Результаты измерений и расчетов для точечного заряда Q = __, = __, (нКл)

Таблица 3. Результаты измерений и расчетов для диполя p₁ = __, p₁^* = __, (∙10^–11 Кл∙м)

Получите у преподавателя допуск для выполнения измерений.

Эксперимент 1. Исследование поля точечного заряда

1.	Зацепив мышью (нажав и удерживая левую кнопку, когда маркер мыши находится над объектом), перемещайте заряд Q1 и зафиксируйте его вблизи левой границы экспериментального поля.
2.	Нажимайте кнопку регулятора величины первого заряда и установите величину заряда Q1 , указанную в табл. 2 для вашей бригады.
3.	Заряд Q3 поместите под первым, а его величину установите равной 0. Заряд Q2 установите равным 100 нКл.
4.	Перемещайте, зацепив мышью, заряд Q2 вправо, устанавливая расстояния r12 до первого заряда, указанные в табл. 2.
5.	Измеренные в данных точках значения F21 и вычисленные Е1 = занесите в соответствующую строку табл. 2.
6.	Повторите измерения для другого значения заряда Q1* из табл. 1, записывая в табл.2 значения F21* и Е1*.

Эксперимент 2. Исследование поля диполя

• Щелкайте мышью кнопку регулятора величины заряда Q₃ и зафикси-руйте значение заряда, равное (и противоположное по знаку) заряду Q₁ (указано в табл. 1 для вашей бригады).
• Переместите заряд Q₃ так, чтобы электрический момент диполя был вертикальным (рис. 3), а плечо диполя (L = r₃₁) было равно 1 см.

  Расположение зарядов при исследовании поля диполя.

• Перемещайте мышью заряд Q₂ по линии, перпендикулярной оси диполя (горизонтально, при этом r₁₂ = r₂₃ = r).
• На расстояниях r от оси диполя, указанных в табл. 3, измерьте F₂₁, вычислите Е = ∙ и занесите значения в табл.3.
• Повторите измерения для другого значения заряда Q₁^* (и Q₃^*) из табл. 1, записывая в табл. 3 значения F₂^* и Е^*.

Вычислите и запишите в табл. 2 и 3 значения всех характеристик.

Постройте на одном листе графики (для каждого Q₁) зависимости логарифма напряженности ЭП точечного заряда (2 графика) и диполя (2 графика) от логарифма расстояния.

По точке пересечения b_i (см. формулы 1 и 2) каждого графика с вертикальной осью определите электрическую постоянную, используя для поля точечного заряда формулу

и для поля диполя

Запишите ответы и проанализируйте ответ и график.