|
Колебательным контуром называется замкнутая цепь, содержащая катушку индуктивности с индуктивностью L , конденсатор с емкостью С и резистор с сопротивлением R.
Напряжение на конденсаторе: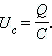 
ЭДС самоиндукции в катушке :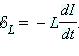 
Напряжение на катушке: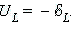 
Напряжение на резисторе: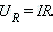 
Определение тока: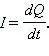 
Если в цепи нет резистора (сопротивление R = 0), то в контуре возможны гармонические (незатухающие) колебания тока I, заряда конденсатора Q и напряжения на элементах. Такие колебания называются свободными незатухающими.
Дифференциальное уравнение свободных незатухающих колебаний заряда конденсатора Q:
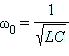– собственная частота контура.
Период колебаний: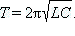 
Его решение имеет вид
где α0 – начальная фаза, Qmax – амплитуда.
Дифференциальное уравнение свободных затухающих колебаний, имеющих место при наличии в контуре резистора c сопротивлением R:
где β =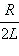 
– коэффициент затухания.
Его решение:
где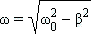 
– частота затухающих колебаний.
Постоянная времени затухания в контуре τ = 1/β есть время, за которое амплитуда колебаний уменьшается в е = 2,73 раз. На графике зависимости амплитуды затухающих колебаний от времени касательная, проведенная к этому графику в начальный момент времени, пересекает ось времени в точке t = τ.
|
|
|
Свободные затухающие колебания заряда конденсатора в контуре
|
Логарифмическим декрементном затухания называется величина, определяемая формулой
Добротность контура равна Q =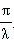 
|
и также внесите в табл. 2.