|
Повторите основные определения для периодического (колебательного) движения и гармонических колебаний. Прочитайте также снова теорию, в которой рассмотрены свободные колебания в контуре.
Колебательным контуром называют замкнутую электрическую цепь, содержащую конденсатор, катушку индуктивности, резистор и источник с переменной ЭДС.
Вынужденными называют колебания в контуре, возникающие при периодическом изменении величины ЭДС источника.
Установившимися называют колебания, амплитуда которых со временем не меняется.
|
|
|
Эквивалентная схема последовательного колебательного контура
|
Если ЭДС источника в контуре меняется по гармоническому закону, то наблюдаются вынужденные гармонические колебания тока и напряжения на отдельных элементах цепи.
Характеристику, меняющуюся со временем по гармоническому закону, иногда удобно описывать с помощью комплексной величины.
Комплексное число (КЧ) есть упорядоченная пара алгебраических чисел. Алгебраическое представление комплексного числа имеет вид суммы двух слагаемых
где
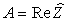 – действительная часть,
– действительная часть, 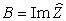 – мнимая часть,
– мнимая часть, 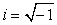 – мнимая единица.
– мнимая единица.
Экспоненциальное представление КЧ выглядит, как произведение
где Z – модуль, φ – фаза комплексного числа.
Оба представления одного комплексного числа связаны друг с другом:
Графически 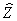 можно изобразить, как радиус-вектор на комплексной плоскости: его длина равна Z, а угол между вектором и горизонтальной (действительной) осью равен φ. Действительная часть КЧ есть проекция радиус-вектора
можно изобразить, как радиус-вектор на комплексной плоскости: его длина равна Z, а угол между вектором и горизонтальной (действительной) осью равен φ. Действительная часть КЧ есть проекция радиус-вектора 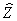 на горизонтальную ось, а мнимая часть – проекция на вертикальную ось. на горизонтальную ось, а мнимая часть – проекция на вертикальную ось.
|
|
|
Графическая интерпретация комплексного числа
|
Комплексный ток и комплексное напряжение
Гармонически изменяющаяся физическая характеристика, например, величина тока зависит от времени по закону синуса или косинуса
Точно такое же выражение получится, если взять комплексный ток в виде
и спроектировать его на горизонтальную ось, т. е.
В чем же удобство комплексных физических характеристик по сравнению с обычными гармоническими? Рассмотрим их более внимательно.
Запишем комплексный ток, используя свойство показательной функции:
Второй сомножитель 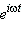 описывает вращение радиус-вектора в комплексной плоскости с угловой скоростью ω, а первый сомножитель (в скобках) является радиус-вектором в начальный момент времени (t = 0). Этот сомножитель, который можно считать мгновенной фотографией вектора в начальный момент времени, получил название комплексная амплитуда (в данном случае величины тока описывает вращение радиус-вектора в комплексной плоскости с угловой скоростью ω, а первый сомножитель (в скобках) является радиус-вектором в начальный момент времени (t = 0). Этот сомножитель, который можно считать мгновенной фотографией вектора в начальный момент времени, получил название комплексная амплитуда (в данном случае величины тока 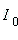 ). ).
Используя понятие комплексной амплитуды, можно записать выражения для комплексных токов и напряжений
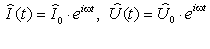 – это радиус-векторы в комплексной плоскости, которые вращаются с угловой скоростью ω. – это радиус-векторы в комплексной плоскости, которые вращаются с угловой скоростью ω.
Здесь 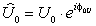 – комплексная амплитуда напряжения;
– комплексная амплитуда напряжения;
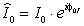 – комплексная амплитуда тока.
– комплексная амплитуда тока.
 и и 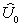 – комплексные векторы, которые на комплексной плоскости неподвижны и составляют углы – комплексные векторы, которые на комплексной плоскости неподвижны и составляют углы  и и 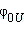 с горизонтальной осью. Они соответствуют «мгновенной фотографии» реальных комплексных токов и напряжений, сделанной в начальный момент времени (t = 0). с горизонтальной осью. Они соответствуют «мгновенной фотографии» реальных комплексных токов и напряжений, сделанной в начальный момент времени (t = 0).
Комплексная амплитуда – сама комплексная величина, взятая в начальный момент времени. Очень часто можно исследовать комплексные амплитуды вместо самих комплексных физических характеристик, что намного удобнее, поскольку радиус-векторы комплексных амплитуд неподвижны.
Рассмотрим некоторый элемент электрической цепи, через который идет гармонический ток I (t) и между клеммами которого есть переменное напряжение U (t). Представим ток и напряжение в комплексном виде:
|
|
|
Схематическое изображение элемента цепи переменного тока
|
Элемент цепи называется линейным, если напряжение на нем и ток через него меняются по гармоническому закону с одной и той же частотой, а амплитуда напряжения пропорциональна амплитуде тока
где Z называется полным электрическим сопротивлением цепи.
Если коэффициент пропорциональности считать комплексным
 то аналогичное соотношение будет выполняться и для комплексных амплитуд
поскольку между комплексными амплитудами тока и напряжения в общем случае существует разность фаз
Из формулы (1) видно, что импеданс – это отношение комплексной амплитуды напряжения на данном элементе, к комплексной амплитуде тока через данный элемент.
Модуль импеданса называется полным электрическим сопротивлением цепи.
Импеданс равен отношению комплексных амплитуд:
где Δφ = φU – φI – разность фаз между напряжением и током на данном элементе. Полное электрическое сопротивление равно отношению «настоящих» амплитуд напряжения и тока.
Полное электрическое сопротивление равно отношению «настоящих» амплитуд напряжения и тока:
Рассмотрим отдельные элементы цепи переменного тока.
| А) |
Резистор:
и, так как фазы напряжения и тока в резисторе совпадают, ΔφR = 0, и импеданс резистора равен R:
|
| Б) |
Катушка индуктивности. По определению
В катушке действует закон электромагнитной индукции (самоиндукции):
Использовав его для комплексных величин, получим:
Пусть 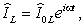 тогда
тогда 
После подстановки в уравнение (3) получим
Для комплексной амплитуды напряжения
После подстановки в уравнение (2) получим импеданс катушки индуктивности
Напряжение на катушке опережает по фазе ток через нее на π/2. |
| В) |
Конденсатор. По определению
Напряжение на конденсаторе: 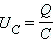 . .
Дифференцируем по времени: 
и переписываем для комплексных величин
Пусть 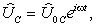
тогда из (5) следует
Комплексная амплитда тока
Подставляем в (4) и находим
отсюда
– комплексное сопротивление (импеданс) конденсатора.
Напряжение на конденсаторе отстает по фазе от тока через него на π/2.
|
Модуль комплексного сопротивления (катушки или конденсатора) называется реактивным сопротивлением (индуктивным или емкостным). Обозначается символом без крышечки над ним.
Для катушки индуктивности 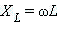 и для конденсатора
и для конденсатора 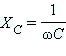 . .
Рассмотрим колебательный контур.
Все элементы в контуре соединены последовательно, поэтому для нахождения импеданса контура надо просуммировать импедансы всех элементов:
После подстановки можем получить модуль импеданса, то есть полное сопротивление контура:
Резонансом для тока называется явление резкого увеличения амплитуды колебаний тока при приближении частоты ЭДС к некоторому значению, называемому резонансной частотой ωрез. Нетрудно видеть, что максимум амплитуды тока будет тогда, когда минимально полное сопротивление контура, или
Отсюда
что соответствует частоте свободных колебаний в контуре.
Максимум напряжения на конденсаторе соответствует резонансу для напряжения, который наблюдается при несколько меньшей частоте ЭДС:
где δ = 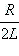 – коэффициент затухания для данного контура.
– коэффициент затухания для данного контура.
Для малых коэффициентов затухания можно использовать приближенное выражение для корня. Тогда
отсюда
где
называется характеристическим сопротивлением контура. Амплитуда резонансного напряжения на конденсаторе U0C пропорциональна амплитуде ЭДС и добротности контура Q:
При не слишком большом затухании в контуре добротность определяется соотношением
Чем больше добротность, тем «острее» резонанс.
Сравнив (1) и (2), получим
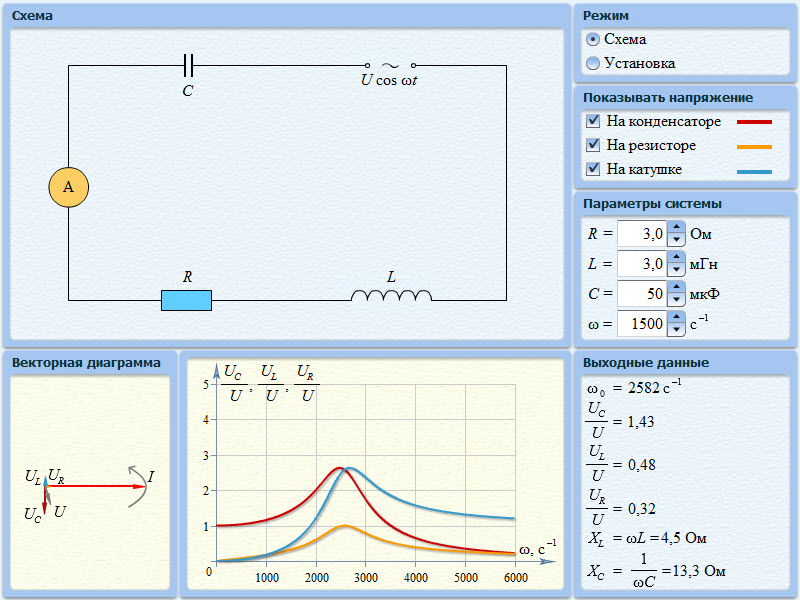
Резонансной кривой напряжения называется зависимость амплитуды напряжения на конденсаторе UC0 от частоты ЭДС (на рис. 4 величина UC0 делится на постоянную величину U, равную амплитуде ЭДС).
 |
|
Модель колебательного контура с источником гармонической ЭДС
|
|