|
Повторите основные определения для периодического (колебательного) движения и гармонических колебаний. Прочитайте также теорию, в которой рассмотрены свободные колебания в контуре.
Колебательным контуром называют замкнутую электрическую цепь, содержащую конденсатор, катушку индуктивности, резистор и источник с переменной ЭДС.
Вынужденными называют колебания в контуре, возникающие при периодическом изменении величины ЭДС источника.
Установившимися называют колебания, амплитуда которых со временем не меняется.
|
|
|
Эквивалентная схема последовательного колебательного контура.
|
Если ЭДС источника в контуре меняется по гармоническому закону, то наблюдаются вынужденные гармонические колебания тока и напряжения на отдельных элементах цепи.
Резонансом в колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний тока (или напряжения на отдельных элементах цепи) в колебательном контуре при приближении циклической частоты ω внешней переменной ЭДС к некоторой частоте ω0, называемой резонансной.
Пусть ЭДС генератора меняется по гармоническому закону
где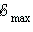 
– амплитуда, 
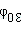– начальная фаза ЭДС.
Тогда установившийся ток в цепи будет меняться тоже по гармоническому закону с частотой ЭДС:
где Imax – амплитуда, φ0I – начальная фаза тока.
В этой цепи возникают вынужденные колебания тока и напряжения на отдельных ее элементах. По определению тока
Для конденсатора
отсюда заряд на конденсаторе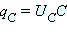 
и ток через конденсатор
Для амплитуд выполняются соотношения
где реактивное сопротивление конденсатора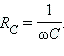 
Аналогичный анализ для катушки индуктивности показывает, что реактивное сопротивление катушки индуктивности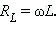 
Полное сопротивление Z цепи, изображенной на рис. 1, определяется формулой:
Амплитуда колебаний тока в цепи будет зависеть от частоты ω приложенного напряжения генератора, так как сопротивления реактивных элементов – конденсатора и катушки индуктивности зависят от частоты:
При низкой частоте ω переменного тока емкостное сопротивление конденсатора будет очень большим, поэтому сила тока в цепи будет мала. В обратном предельном случае большой частоты ω переменного тока большим будет индуктивное сопротивление катушки, и сила тока в цепи опять будет мала.
Ясно, что максимальная сила тока в цепи будет соответствовать такой частоте ω0 приложенного переменного напряжения, при которой полное сопротивление Z будет минимальным (Z = R), а индуктивное и ёмкостное сопротивления будут одинаковы:
При равенстве реактивных сопротивлений катушки и конденсатора, амплитуды напряжений на этих элементах также будут одинаковыми
Колебания напряжения на катушке и конденсаторе противоположны по фазе, поэтому сумма напряжений на катушке и конденсаторе при выполнении условия (1) будет равна нулю.
При очень малом внутреннем сопротивлении источника напряжение на клеммах генератора U близко к ЭДС, поэтому далее будем считать его равным ЭДС.
При резонансе напряжение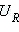 
на резисторе 
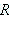будет равно ЭДС, а сила тока в цепи достигнет максимального значения 
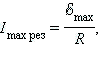называемого резонансным.
Из (1) можно вывести формулу циклической частоты ω0 резонанса, называемого резонансом напряжений:
Она совпадает с циклической частотой свободных незатухающих электромагнитных колебаний в электрическом контуре.
|
|
|
Резонансные кривые тока при различных сопротивлениях резистора
|
Частота ω = ω0 называется резонансной циклической частотой. Резонансная циклическая частота не зависит от активного сопротивления R. График зависимости Imax от ω называется резонансной кривой тока. Резонансные кривые имеют тем более острый максимум, чем меньше активное сопротивление.
Максимум напряжения на конденсаторе соответствует резонансу для напряжения, который наблюдается при несколько меньшей частоте ЭДС:
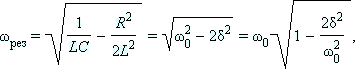 где δ =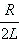 
– коэффициент затухания для данного контура.
Для малых коэффициентов затухания можно использовать приближенное выражение для корня. Тогда
отсюда
где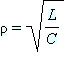 
называется характеристическим сопротивлением контура. Амплитуда резонансного напряжения на конденсаторе U0C пропорциональна амплитуде ЭДС и добротности контура Q:
При не слишком большом затухании в контуре добротность определяется соотношением
Чем больше добротность, тем «острее» резонанс.
Сравнив (1) и (2), получим
Резонансной кривой напряжения называется зависимость амплитуды напряжения на конденсаторе UC0 от частоты ЭДС (на рис. 4 величина UC0 делится на постоянную величину U, равную амплитуде ЭДС).
|
|
|
0 вместо