|
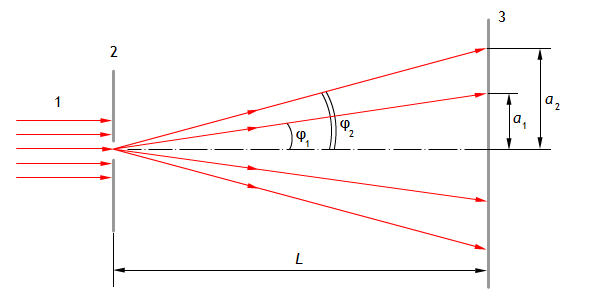
Дифракция Фраунгофера наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Схема наблюдения дифракции Фраунгофера от одной щели показана на рис. 1.
 |
|
Рис. 1
|
Параллельный монохроматический пучок света 1 падает нормально на щель 2, длина которой много больше её ширины d. Согласно принципу Гюйгенса, каждая точка плоскости щели, до которой дошло световое колебание, становится источником вторичных волн, распространяющихся во все стороны под углами дифракции φ1, φ2, …, то есть свет дифрагирует при прохождении через щель. Дифрагированные пучки являются когерентными и могут интерферировать при наложении. Результат интерференции в виде полос с периодическим распределением интенсивности наблюдается на экране 3, находящемся на расстоянии L. Условие дифракционного максимума на основе метода зон Френеля определяется формулой
Более точный расчёт интерференционной картины от одной щели даёт следующие формулы, определяющие углы дифракции, соответствующие дифракционным максимумам:
|
|
первого порядка: d sin φ1 = ±1,43λ;
второго порядка: d sin φ1 = ±2,46λ;
третьего порядка: d sin φ1 = ±3,47λ. |
|
(1)
|
Из этих формул, зная ширину щели d и длину волны света λ, можно теоретически рассчитать направления на точки экрана, в которых амплитуда, а, следовательно, и интенсивность света максимальна. Аналогичные расчёты можно сделать из экспериментальных данных по измеренным на опыте значениям φ1, φ2 и φ3 и заданному расстоянию между щелью и экраном L: (для малых углов допускаем sin φ = tg φ). Тогда:
|