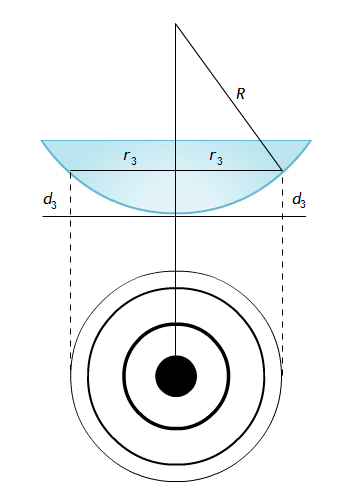
|
Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис. 1).
 |
|
Рис. 1
|
Если на линзу падает пучок монохроматического света, то световые волны, отражённые от верхней и нижней поверхностей воздушной прослойки, будут интерферировать между собой. При этом образуются интерференционные полосы, имеющие форму концентрических светлых и тёмных колец убывающей ширины.
В отражённом свете оптическая разность хода с учётом потери полуволны будет равна
где d – толщина воздушного зазора. Из рис. 1 следует, что
Учитывая, что d2 является величиной второго порядка малости, то из (2) получим
Следовательно,
В точках, для которых оптическая разность хода равна
возникают тёмные кольца. Из формул (4) и (5) радиус k-го тёмного кольца будет равен
Формула (6) позволяет определить радиус кривизны линзы:
Вследствие деформации стекла, а также наличия на стекле пылинок невозможно добиться плотного примыкания линзы и пластины в одной точке. Поэтому при определении радиуса кривизны линзы пользуются другой формулой, в которую входит комбинация из двух значений радиусов интерференционных колец rm и rn, что позволяет исключить возможный зазор в точке контакта линзы и стеклянной пластины:
|
и указанному 
и 
и запишите эти значения в таблицу 2.
