|
Напряжённость электростатического поля в данной точке есть векторная физическая величина, равная отношению силы 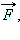 действующей со стороны поля на неподвижный точечный заряд q0, помещённый в данную точку поля, к величине этого заряда: действующей со стороны поля на неподвижный точечный заряд q0, помещённый в данную точку поля, к величине этого заряда:
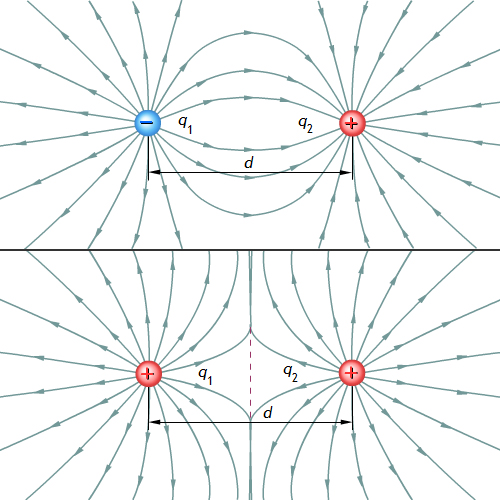
Линиями напряжённости (силовыми линиями) называются линии, проведённые в поле так, что касательные к ним в каждой точке совпадают по направлению с вектором напряжённости. Линии напряжённости проводят так, что они начинаются на положительных зарядах и оканчиваются на отрицательных или уходят в бесконечность (рис. 1).
 |
|
Рис. 1. Линии напряжённости двух точечных зарядов: а) разноимённых; б) одноимённых
|
Принцип супрпозиции электростатических полей: напряжённость электростатического поля систем точечных зарядов равна векторной сумме напряжённостей полей каждого из этих зарядов в отдельности:
Поток вектора напряжённости.
Силовая линия, определяя направление вектора напряжённости, сама по себе не определяет величину модуля вектора напряжённости. Введём условие, связывающее величину модуля вектора напряжённости с числом проводимых линий напряжённости через единицу площади. Для этого выделим в электростатическом поле малую область, в пределах которой электростатическое поле можно считать однородным. Проведём в этой области элементарную площадку dS0, перпендикулярную к линиям напряжённости. Условимся через эту площадку проводить такое число dΦ линий напряжённости, чтобы число линий, приходящихся на единицу поверхности площадки dS0, равнялось величине модуля вектора напряжённости в области этой площадки, то есть потребуем выполнения условия:
При выполнении этого условия графического изображения электростатических полей численное значение вектора напряжённости будет связано с густотой линий напряжённости. Тогда число линий напряжённости, пронизывающих элементарную площадку dS, нормаль 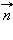 которой образует угол α с вектором которой образует угол α с вектором 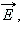 равно равно
где величина dФ называется потоком вектора напряжённости через площадку dS.
Число линий напряжённости Ф, пронизывающих некоторую поверхность S, назовём потоком вектора напряжённости через эту поверхность. Для произвольной замкнутой поверхности S поток вектора E сквозь эту поверхность будет равен
Для замкнутой поверхности принято считать положительным направление нормали к элементу поверхности, выходящее из объёма, ограничиваемого поверхностью. Тогда линии напряжённости, выходящие из объёма, создадут положительный поток Ф+, линии, входящие в объём, создадут отрицательный поток Ф–, а результирующий поток будет равен алгебраической сумме этих потоков.
Теорема Остроградского–Гаусса: поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённой на ε0.
|